Introduction to Euclidian Geometry: Creating an equilateral triangle from scratch

Euclid’s Elements is a geometry text book where figures are constructed using a straightedge a compass. This post is about the first proposition in the Elements; creating an equilateral triangle from scratch.

Learning to do this is a nice introduction to constructive geometry, which is a hands-on way to do mathematics.

Equilateral triangles

the Elements was written by Euclid over two millenia ago (300 BC), and was until around a century ago the standard text boox for geometry in many parts of the world, and is considered one of the most influental text books ever written.

It consists of 13 books (which are more like “parts” of a single book, my copy of all 13 books is only 500 pages long), where the first book is about various constructions of triangles.

The first of these is an equilateral triangle:

A triangle is equilateral if all three sides of it are equal to each other in length.

Geometric construction using straightedge and compass

All the figures in the Elements are constructed using the straightedge and a compass (and some kind of drawing tool, like a pen).

A straightedge is like a ruler without markings on it, and is used to draw straight lines (but not to measure them), and a compass is a two-legged tool for drawing circles, by fixing one leg in a point and spinning the other leg around (with a pen attached).

When working with a straightedge and compass, we also have to have some plane to draw onto. This could be a blackboard, a piece of paper, the sand at the beach, or a computer screen.

This plane is refered to as the ambient plane since it’s not a plane we’ve constructed ourselves, rather it’s assumed to be there in the background.

Using the straightedge and compass

In the Elements, a couple of statements called the “postulates” describe what can be done with a straightedge and a compass. We’ll use Postulate 1 and Postulate 3.

Postulate 1. To draw a straight line from any point to any point.

Although not explicit in the Elements, we can safely assume that we can form a point anywhere we want by placing our drawing tool onto the ambient plane (placing a pen on a sheet of paper).

A point is denoted using a single capital letter, like $A$ or $B$.

Once we have two points, we can join them together into a line segment using the straightedge. If the segment was formed from points $A$ and $B$, it’s denoted $AB$.

Postulate 3. To describe a circle with any center and radius.

The compass can create a circle from a given line segment, by placing each leg on the respective end points of the segment, and spinning the compass around the fixed leg.

The point that the compass fixes on is called the circle’s center, and the line segment is called its radius.

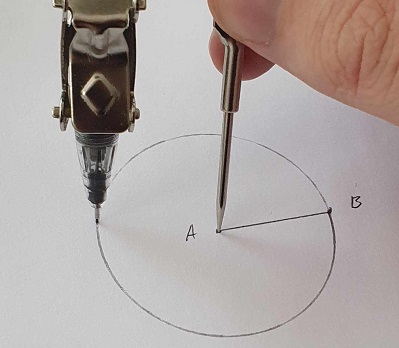
The same circle can have any number of radii, since we can draw any number of segments from the center out to the circle. Each of these radii will equal each other in length.

We refer to a circle by its center point, prefixed with a ring, like $\bigcirc A$.

Constructing the triangle

We now have tools and know how to use them, so we can start with constructing the equilateral triangle.

The theory of the Elements is presented through a series of problems and solutions, where each problem is called a proposition. Each proposition begins with a statement of what is to be done, where the first proposition states the following problem:

To construct an equilateral triangle on a given finite straight line.

The premise of this problem is that there is pre-existing line segment given, and that a triangle is to be constructed from this segment where each side equal the others in length.

Since we don’t have a line segment yet, we’ll create two points $A$ and $B$ and join them into a segment $AB$ using Postulate 1:

Then we use Postulate 3 to create a circle $\bigcirc A$, with point $A$ as center and segment $AB$ as radius:

And then do the same with point $B$ and segment $AB$ to form circle $\bigcirc B$:

We now have two circles, and can note that they’re overlapping each other.

When working with pen and paper, we can focus our eyes on where the circles are intersecting, and place the pen as close as possible to the intersection and form a point there.

In the idealized case, we assume that we have perfect eye sight, and can place a point exactly at the intersection.

The point of intersection above segment $AB$ will be called $C$:

Let’s now use Postulate 1 and this new point $C$ to form two more segments $AC$ and $BC$:

The finished result is this triangle:

This concludes the construction.

Verifying that the construction is correct

Given the triangle that was constructed, we may ask: is it an equilateral triangle?

Since the figure consists of three segments, we know that it is a triangle. Next, we’ll prove that these three sides all equal each other.

Equality of $AB$ and $AC$

We’ll start by claiming that $AB$ and $AC$ are equal segments:

To show that this is true, we can first observe that the segments $AB$ and $AC$ are both radii to the same circle $\bigcirc A$:

We can recall that we previously stated that all radii of the same circle are equal, so consequently we now know that $AB$ and $AC$ are equal.

Equality of $AB$ and $BC$

The second claim we’ll make is that $AB$ and $BC$ are equal:

This follows by the same argument as we made for $\eqref{eq:ab-ac}$, by observing that the figure is symmetrical, such that both $AB$ and $BC$ are equal radii to circle $\bigcirc B$:

Because of this symmetry, we now know that $AB$ and $BC$ are equal.

Equality of $AC$ and $BC$

The third equality we’ll claim is the following:

To prove this we’ll use an axiom from Elements, where an axiom is a statement that is accepted as true as the basis for an argument.

Axiom 1 of the Elements reads:

Things which equal the same thing also equal one another.

This says that if we know that $X$ is equal to $Y$, and $X$ is equal to $Z$, then we can combine these two facts to know that $Y$ is equal to $Z$.

Formally, this can be written schematically like this:

The statements above the line are called the premises, and the statement below the line is called the conclusion.

If, after substituting the variables $X$, $Y$, and $Z$, the premises are true, then the conclusion will also be true.

We can plug in equations $\eqref{eq:ab-ac}$, $\eqref{eq:ab-bc}$ and $\eqref{eq:ac-bc}$ into Axiom 1 to get:

Since $AC$ is the same length as $AB$, and $BC$ is the same length as $AB$, then that means that $AC$ and $BC$ have the same length.

So, we now know that $AC = BC$.

Equality of all three sides

We now know all three of the statements $AB = AC$, $AB = BC$ and $AC = BC$.

Consequently we know that $AB = AC = BC$.

In other words, we know that all three sides of the triangle we constructed are equal each to other.

This means that the triangle we constructed from the line segment is equilateral, which was what we wanted to do.

This concludes the proof.

$ \text{Q.E.F.} $

Composing propositions

In this post, we first constructed a figure through a sequence of explicit steps, and then we analyzed the construction to show that it had all the desired properties.

Most problems in the Elements are solved in this style:

1. A figure is constructed
2. Properties of the figure is proved

Each of the propositions in the Elements build upon earlier ones, where the figure that is to be constructed uses steps from other propositions as building blocks.

Already in Proposition 2, where a given line segment $BC$ is to be moved to coincide with a given point $A$, one of the steps is to use Proposition 1 to form an equilateral triangle $\Delta ABD$ from line $AB$.

Not only are the constructions composable, but the proofs also compose.

We can rely on all the properties of the equilateral triangle that was shown in Proposition 1 when reasoning about the properties of the construction in Proposition 2.

Every proposition in the Elements build upon the previous ones in this fashion.

Constructive geometry and computer programs

The equilateral triangle was constructed through a series of explicit instructions that had the line segment $AB$ as a premise. Another way of viewing this is that the segment is a parameter of the construction, which we can view as a sort of procedure, that accepts a segment and produces a triangle:

The way propositions in the Elements are built up by using earlier propositions has a parallel to how functions in computer programs are composed out of other functions.

The construction in Proposition 1 can be expressed with this psuedocode:

function equilateral_triangle({a, b}: Segment) {
    let circle_a = Circle(a, {a, b})
    let circle_b = Circle(b, {a, b})
    let c = intersection(circle_a, circle_b)[0] // pick first intersection
    return Triangle(a, b, c)
}

We can then imagine psuedocode for other propositions calling this function:

let abc = equilateral_triangle({a, b})

Working through the Elements, you get a sense how something big and complex can be built out of smaller parts, and how we can have an understanding of that complex thing through our understanding of those parts.

Closing remarks

If you enjoyed this post, I encourage you to get hold of a ruler and a compass and trying out this construction for yourself. Reading about math is one thing, practicing it is another!

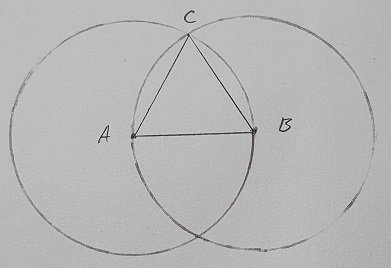
Once you get the hang of drawing circles with the compass, it’ll just take a few seconds to draw this, and it’s a very satisfying thing to do.